Integral (Pengertian dan Konsep) - Part 1

Apa sih integral itu ? kenapa dirimu begitu susah dikerjakan ?

Sebenernya sih nggak susah cuman kita belum kenal aja sama beliau, maka dari itu pertama yuk kita pelajari cerita hidup si integral ini. sebenarnya si integral ini tidak jelas asal muasalnya banyak sekali ilmuan di masa yang berbeda diklaim sebagai penemu atau bapak dari integral itu sendiri. salah seorang yang diklaim sebagai penemu integral itu sendiri ialah dari ilmuan berkebangsaan yunani yang bernama Archimedes. Pertama kali integral ini digunakan untuk menentukan luas sebuah daerah tertutup dan volume dari benda putar diantaranya adalah rumus lingkaran, luas segmen parabola, volume  bola, volume kerucut, serta benda-benda yang dapat berputar lainnya. itulah awal pertama tenarnya si integral ini.

Pengertian Intergral:

Menurut Wikipedia Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika, dan bersama dengan inversnya, diferensiasi, dan adalah satu dari dua operasi utama dalam kalkulus.

Integral dikembangkan menyusul ditemukannya masalah dalam diferensiasi dimana matematikawan harus berfikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. Lambang integral adalah 

Biarpun asalnya tidak jelas, integral ini memiliki banyak sekali kegunaan dan telah banyak diaplikasikan demi keuntungan manusia, diantaranya pada bidang:

1. Ekonomi; mencari biaya total, mencari fungsi penerimaan total, mencari fungsi konsumsi, fungsi tabungan, beserta fungsi-fungsi marginalnya, dan masih banyak lagi.
2. Teknologi; memecahkan persoalan yang berkaitan dengan volume, panjang kurva, keluaran kardiak, gaya pada bendungan, usaha, dll.
3. Fisika; alat analisis rangkaian listrik, medan magnet pada kumparan, gaya pada struktur pelengkung, dll.
4. dan masih banyak lagi yang lainnya.

Banyak kan aplikasi integral pada kehidupan sehari-hari. jadi yuk semangatnya kita tambah lagi buat masuk konsep dasar perhitungannya.

pertama-tama yuk kita pelajari integral tak tentu, integral tak tentu digunakan untuk menghitung limit dari jumlah atau untuk mengetahui invers dari turunan. berikut ini ialah rumus integral tak tentu.

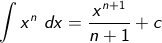jadi bagaimana cara menghitung integral ? yuk langsung saja kita coba hitung. misal seperti ini:

Pada persoalan diatas hanya ada satu persamaan saja. pada nyatanya integral juga dapat diterapkan dalam operasi penjumlahan persamaan. berikut ialah contoh persamaan integral dasar yang akan banyak kita temui:

Berikut disajikan contoh dan penyelesaian untuk bentuk penjumlahan dan pengurangan.

ini belum termasuk integral dengan perkalian, pembagian, dan lain sebagainya. tapi jangan takut dulu kita akan mengupas habis semuanya pada blog ini. tapi kali ini, kita akhiri sampai di sini dulu. untuk penjelasan mengenai integral ini kita sambung pada pos yang lain.

Part II  >>

Sumber:

Wikipedia.org

Matematikastudycenter.com